Mirror symmetry (string theory)
In physics and mathematics, mirror symmetry is a relation that can exist between two Calabi-Yau manifolds. It happens, usually for two such six-dimensional manifolds, that the shapes may look very different geometrically, but nevertheless they are equivalent if they are employed as hidden dimensions of string theory. The classical formulation of mirror symmetry relates two Calabi-Yau threefolds M and W whose Hodge numbers h1,1 and h1,2 are swapped; string theory compactified on these two manifolds lead to identical effective field theories.
Contents |
History
The discovery of mirror symmetry is connected with names such as Lance Dixon, Wolfgang Lerche, Cumrun Vafa, Nicholas Warner, Brian Greene, Ronen Plesser, Philip Candelas, Monika Lynker, Rolf Schimmrigk and others. Andrew Strominger, Shing-Tung Yau, and Eric Zaslow have showed that mirror symmetry is a special example of T-duality: the Calabi-Yau manifold may be written as a fiber bundle whose fiber is a three-dimensional torus. The simultaneous action of T-duality on all three dimensions of this torus is equivalent to mirror symmetry.
Mathematicians became interested in mirror symmetry in 1990, after Candelas-de la Ossa-Green-Parkes gave predictions for numbers of rational curves in a quintic threefold via data coming from variation of Hodge structure on the mirror family. These predictions were mathematically proven a few years later by Alexander Givental and Lian-Liu-Yau.
Applications
Mirror symmetry allowed the physicists to calculate many quantities that seemed virtually incalculable before, by invoking the "mirror" description of a given physical situation, which can be often much easier. Mirror symmetry has also become a tool in mathematics, and although mathematicians have proved theorems based on the physicists' intuition, a full mathematical understanding of the phenomenon of mirror symmetry is still being developed.
Most of the physical examples can be conceptualized by the Batyrev-Borisov mirror construction, which uses the duality of reflexive polytopes and nef partitions. In their construction the mirror partners appear as anticanonically embedded hypersurfaces or certain complete intersections in Fano toric varieties. The Gross-Siebert mirror construction generalizes this to non-embedded cases by looking at degenerating families of Calabi-Yau manifolds. This point of view also includes T-duality. Another mathematical framework is provided by the homological mirror symmetry conjecture.
Generalizations
There are two different, but closely related, string theory statements of mirror symmetry.[1]
- 1. Type IIA string theory on a Calabi-Yau M is mirror dual to Type IIB on W.
- 2. Type IIB string theory on a Calabi-Yau M is mirror dual to Type IIA on W.
This follows from the fact that Calabi-Yau hodge numbers satisfy h1,1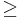 1 but h2,1
1 but h2,1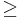 0. If the Hodge numbers of M are such that h2,1=0 then by definition its mirror dual W is not Calabi-Yau. As a result mirror symmetry allows for the definition of an extended space of compact spaces, which are defined by the W of the above two mirror symmetries.
0. If the Hodge numbers of M are such that h2,1=0 then by definition its mirror dual W is not Calabi-Yau. As a result mirror symmetry allows for the definition of an extended space of compact spaces, which are defined by the W of the above two mirror symmetries.
Mirror symmetry has also been generalized to a duality between supersymmetric gauge theories in various numbers of dimensions. In this generalized context the original mirror symmetry, which relates pairs of toric Calabi-Yau manifolds, relates the moduli spaces of 2-dimensional abelian supersymmetric gauge theories when the sums of the electric charges of the matter are equal to zero.
In all manifestations of mirror symmetry found so far a central role is played by the fact that in a d-dimensional quantum field theory a differential p-form potential admits a dual formulation as a (d-p-2)-form potential. In 4-dimensions this relates the electric and magnetic vector potentials and is called electric-magnetic duality. In 3-dimensions this duality relates a vector and a scalar, which in an abelian gauge theory correspond to a photon and a squark. In 2-dimensions it relates two scalars, but while one carries an electric charge, the dual scalar is an uncharged Fayet-Iliopoulos term. In the process of this duality topological solitons called Abrikosov-Nielsen-Oleson vortices are intercharged with elementary quark fields in the 3-dimensional case and play the role in instantons in the 2-dimensional case.
The derivations of 2-dimensional mirror symmetry and 3-dimensional mirror symmetry are both inspired by Alexander Polyakov's instanton calculation in non-supersymmetric quantum electrodynamics with a scalar Higgs field. In a 1977 article[2] he demonstrated that instanton effects give the photon a mass, where the instanton is a 't Hooft-Polyakov monopole embedded in an ultraviolet nonabelian gauge group.
Mirror symmetry in 2-dimensional gauged sigma models
Mirror symmetries in 2-dimensional sigma models are usually considered in cases with N=(2,2) supersymmetry, which means that the fermionic supersymmetry generators are the four real components of a single Dirac spinor. This is the case which is relevant, for example, to topological string theories and type II superstring theory. Generalizations to N=(2,0) supersymmetry have also appeared.[3]
The matter content of N=(2,2) gauged linear sigma models consists of three kinds of supermultiplet. The gauge bosons occur in vector multiplets, the charged matter occurs in chiral multiplets and the Fayet-Ilipolous (FI) terms of the various abelian gauge symmetries occur in twisted chiral multiplets. Mirror symmetry exchanges chiral and twisted chiral multiplets.
Mirror symmetry, in a class of models of toric varieties with zero first Chern class Calabi-Yau manifolds and positive first Chern class (Fano varieties) was proven by Kentaro Hori and Cumrun Vafa.[4] Their approach is as follows. A sigma model whose target space is a toric variety may be described by an abelian gauge theory with charged chiral multiplets. Mirror symmetry then replaces these charged chiral multiplets with uncharged twisted chiral multiplets whose vacuum expectation values are FI terms. Instantons in the dual theory are now vortices whose action is given by the exponential of the FI term. These vortices each have precisely 2 fermion zeromodes, and so the sole correction to the superpotential is given by a single vortex. The nonperturbative corrections to the dual superpotential may then be found by simply summing the exponentials of the FI terms. Therefore mirror symmetry allows one to find the full nonperturbative solutions to the theory.
In addition to finding many new dualities, this allowed them to demonstrate many dualities that had been conjectured in the literature. For example, beginning with a sigma model whose target space is the 2-sphere they found an exactly solvable Sine-Gordon model. More generally, when the original sigma model's target space is the n-complex dimensional projective space they found that the dual theory is the exactly solvable affine Toda model.
Mirror symmetry in 3-dimensional gauge theories
Mirror symmetry in 3-dimensional gauge theories with N=4 supersymmetry, or 8 supercharges, was first proposed by Kenneth Intriligator and Nathan Seiberg in their 1996 paper[5] as a relation between pairs of 3-dimensional gauge theories such that the Coulomb branch of the moduli space of one is the Higgs branch of the moduli space of the other. It was demonstrated using D-brane cartoons by Amihay Hanany and Edward Witten 4 months later,[6] where they found that it is a consequence of S-duality in type IIB string theory.
Four months later it was extended to N=2 gauge theories resulting from supersymmetry breaking in N=4 theories.[7] Here it was given a physical interpretation in terms of vortices. Vortices in 3-dimensional gauge theories are particles. BPS vortices, which are those vortices that preserve some supersymmetry, have masses which are given by the FI term of the gauge theory. In particular, on the Higgs branch, where the squarks are massless and condense yielding nontrivial vacuum expectation values (VEVs), the vortices are massive. On the other hand they interpret the Coulomb branch of the gauge theory, where the scalar in the vector multiplet has a VEV, as being the regime where massless vortices condense. Thus the duality between the Coulumb branch in one theory and the Higgs branch in the dual theory is the duality between squarks and vortices.
In this theory the instantons are 't Hooft-Polyakov magnetic monopoles, whose actions are proportional to the VEV of the scalar in the vector multiplet. In this case instanton calculations again reproduce the nonperturbative superpotential. In particular, in the N=4 case with SU(2) gauge symmetry, the metric on the moduli space was found by Nathan Seiberg and Edward Witten[8] using holomorphy and supersymmetric nonrenormalization theorems several days before Intriligator and Seiberg's 3-dimensional mirror symmetry paper appeared. Their results were reproduced using standard instanton techniques.[9]
Notes
- ^ In Section 9.9 of 'String Theory and M theory' by Becker, Becker and Schwarz
- ^ Quark Confinement and Topology of Gauge Groups
- ^ For example in (0,2) duality.
- ^ In the paper Mirror Symmetry.
- ^ Mirror symmetry in three-dimensional gauge theories
- ^ In Type IIB superstrings, BPS monopoles, and three-dimensional gauge dynamics
- ^ In the article Aspects of N=2 supersymmetric gauge theories in three-dimensions.
- ^ In Gauge dynamics and compactification to three-dimensions
- ^ In Instanton effects in three-dimensional supersymmetric gauge theories with matter
References
- Strominger, Andrew; Yau, Shing-Tung; Zaslow, Eric, "Mirror Symmetry is T-duality" hep-th/9606040
- Cox, David A.; Katz, Sheldon, Mirror symmetry and algebraic geometry. Mathematical Surveys and Monographs, 68. American Mathematical Society, Providence, RI, 1999. xxii+469 pp. ISBN 0-8218-1059-6
- Hori, Kentaro; Katz, Sheldon; Klemm, Albrecht; Pandharipande, Rahul; Thomas, Richard; Vafa, Cumrun; Vakil, Ravi; Zaslow, Eric Mirror symmetry. Clay Mathematics Monographs, 1. American Mathematical Society, Providence, RI; Clay Mathematics Institute, Cambridge, MA, 2003. xx+929 pp. ISBN 0-8218-2955-6
- Victor Batyrev; Dual Polyhedra and Mirror Symmetry for Calabi-Yau Hypersurfaces in Toric Varieties J. Algebraic Geom. 3 (1994), no. 3, 493—535
- Mark Gross; Toric Degenerations and Batyrev-Borisov Duality: [1]